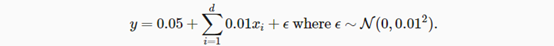D2DL笔记_5
数据集的使用
图像分类数据集:MNIST
但是过于简单,教材使用了类似但更复杂一些的Fashion-MNIST数据集
首先加载一些包:
(%matplotlib inline是在jupyter画图用的,如果不是jupyter如pycharm的话,是不需要这一行的)
先把transforms转成张量形式,否则所有数据返回的是PIL图片,再调用Fashion-MNIST数据集,分别看一下train和test的数据量(会有下载过程,很快,数据集就两百多兆的样子,root=”./data”的意思是在该python文件的上一级目录中新建一个data文件夹):
训练集和测试集大小:
调用第一个图看看,[0][0]第一个0表示训练集中的第0个图,第二个0表示这张图的张量信息,是一个三维张量,分别表示图的RGB信息,而1的话就是图的标号(label):
将数据集可视化:
Next取第一个批量的18个数据进行可视化:
读取一小批数据,大小为batch_size,用4个进程读取,查看消耗的时间:
一般在训练模型之前需要测试一下设备读取数据的速度,读取的速度至少要和训练的速度差不多,最好是读取速度比训练速度快很多,避免出现来不及读取的情况。
最后把之前搞的一些零零碎碎的小函数整合一下,此外还添加了一个resize功能,因为Fashion-MNIST数据集都是28 x 28大小的图片,而别的数据集则有各种尺寸的图像,为了提高函数的泛用性,最好可以resize,直接对transforms做resize就可以了:
Softmax回归的实现(虽然softmax叫回归,但实际上更像一个分类器,因为它是多输入多输出的,而回归问题通常只有一个输出)
由于Fashion-MNIST数据集的图像的形式都是三维的张量,而softmax的输入要求是向量,所以我们需要把图像拉长,长度为28 x 28 = 784,又因为数据集的图像有10个类别,所以网络的输出维度设为10(其实拉伸向量会使它损失掉很多空间信息,后面相似的问题会在卷积神经网络中进行处理),接着初始化权重w和偏移b,并做好计算梯度的准备,初始化的时候需要注意权重w的形状:
实现softmax:
由于X是矩阵,所以对每一行做Softmax,也就是对每一行求和,同时注意保持维度不变,这样就可以利用广播机制,对X_exp中的每一行除以对应的partition(借由广播机制,可以省去循环的设计):
测试一下softmax函数:
可见softmax因为keepdim而没有改变X的形状(均值为0,方差为1),仍然是二行五列,而且每个元素都变成了正值且每一行的和为1(在行上做的softmax,每一项都是一个概率,所有项的和自然为100%,也就是1。机器学习/深度学习就是一直求各种概率的过程)。
定义一下softmax回归模型:
Reshape-1的意思是让torch自己确认需要多少行,然后取权重相同的列,做矩阵乘法,最后加上偏移b送到softmax里面:
接下来计算交叉熵损失:
首先需要解决的问题是,如何从预测值里面把和真实值y对应的y_hat拿出来:
通过假设简化问题,假设我们有两个真实数据,总共有三个不同的类别(0,1,2),y很当然得由两个真实值组成一个长为2的向量(第一个是第0类,第二个是第2类),而y_hat就会是一个两行三列的矩阵,两行表示对两个真实值的预测,三列分别存储该个体属于0 or 1 or 2类的概率。y_hat[[0, 1], y]的意思是,根据标号0去y里面把第0个样本的真实种类(第0类)在y_hat中对应的概率(0.1)拿出来,对标号1同理:
(其实也就是y_hat[[0, 1], [0, 2]],取y_hat中第0行第0列和第1行第2列的数据)
实现交叉熵损失:
将预测值和真实值作比较:
首先要确认y_hat中有多类的概率预测,然后把其中每一行概率最大的下标(也就是种类)传给y_hat,最后将y_hat与y比较,判断类型是否相同,将true or false传给cmp形成一个布尔类型的变量,再将其转为float类型:
可以算一下准确率:
结果是0.5,因为这之前的预测是随机的。
可以用一样的方法算任意模型预测的准确率:
Accumulator()是一个累加器,在n个变量上累加:
可以看一下evaluate的结果:
因为总共分了十个类,而预测是随机的,所以准确率应该在10%(0.10)左右。
Softmax训练(这里直接贴教材上的代码,有注释):
训练数据可视化(画图函数):
以下是训练模型:
学习率设置为0.1,最后使用随机梯度下降:
训练10个epoch(还没有完全收敛):
对图像分类进行预测:
其中交叉熵和softmax模型的实现可以直接调用nn.CrossEntropyLoss()实现,简洁不是一点半点。
感知机
感知机其实是人工智能领域最早的模型。
原始的感知机其实是一个二分类问题,一般是分成正类和负类两种。又因为在二维层面上,感知机只能生成线性分割面,所以它处理不了XOR(异或)问题,比如一个平面坐标系表示的样本空间被四个象限所划分,两个类四个样本分别分布在每个象限中,一三象限的样本实际上是一类,二四象限的样本实际上是一类,这种情况下,是无法直接通过一个线性分割面(也就是感知机)去划分的。
对于XOR问题,可以通过升维的方式升到高维的特征空间,再通过超平面去划分,到实际操作上来说就是经过多次二分类分割再做异或来综合的方式解决(多层感知机MLP)。
训练感知机(伪代码):
initialize w = 0 and b = 0
repeat
if y_i * [<w, x_i> + b] <= 0 then
w <- w + y_i * x_i and b <- b + y_i
end if
until all classified correctly
等价于使用批量大小为1的梯度下降(因为感知机会一直repeat到所有样本都分类正确,不是随机的,所以不等价于随机梯度下降)
多层感知机
结构图:
输入肯定是训练数据集规定好的,输出也是根据实际需要规定好的,都是固定的,多层感知机可以做调整的就是隐藏层的层数和每个隐藏层的大小,这些是超参数,理论上讲需要手动调整。
多层感知机的实现:
批量大小设置成256,和前面一样。
变量初始化:
输入是28 x 28 = 784,输出是10,这两个值是固定的,一个有数据集输入的规模决定,一个由输出的实际需求决定。
隐藏层的大小是超参数,手动设置为256。
这里是只有一层隐藏层的情况。
W1的行是输入大小,列是隐藏层数,随机取是为了让模型能够学得动,如果置0的话,w1会不能更新,一直是0,因为是随机取值,所以*0.01稳住方差。
ReLU函数,也就是max(0, x),一种很简单的激活函数,计算简洁,和sigmoid、tanh相比的话,不需要进行指数运算,节约运算开销,而且可以避免梯度爆炸或者梯度消失,此外其实对模型精度的提高的帮助并不太大,只是因为简单好用,所以挺多人用ReLU做激活函数:
模型的实现:
其中,@符号表示矩阵乘法,之前有用过mm函数,用@的话表达式会更简洁。
损失函数跟之前一样,使用CrossEntropy:
训练模型:
由于多层感知机其实也可以看作是一种多分类问题,softmax也可以看作多分类问题,所以在训练的时候,他俩的操作是一样的,可以直接调用d2l中之前对softmax训练的train_ch3函数来训练,这也是目前MLP的使用范围比SVM更广的一个原因,因为MLP可以很简单地把网络换成CNN、RNN、transformer等而不需要重新调太多参,此外,SVM学不了很大的数据,而且可以调节的超参数不多,所以深度学习里面涉及很少,这是主要原因。
这里跑10个epoch,learning rate选0.1:
可以看到多层感知机想比之前softmax的训练结果来说,损失loss虽然下降了,但是精度却没有明显的提升,这是因为多层感知机的模型比softmax的来说更大了,所以模型在拟合数据上的损失变小了,但是由于回归策略是一样的,所以精度上都差不多。所以无论是尝试增大批量大小还是减小学习率,只能将损失再次降低,却不会提高精度。
多层感知机也可以调用现成的API来实现,但是也就是精简了ReLU函数和模型部分的一些代码。