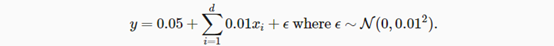D2DL笔记_4

梯度：

在标量导数的基础上，将导数拓展到向量层面，称为梯度（gradient），梯度就是函数的这一点在梯度的方向上变化率最大，变化最快，所以机器学习/深度学习中，经常需要求梯度来优化模型。

（理解一下就好，不常用到）y是x的函数：

对于y对x向量的偏导而言，

求导就是为了得到指向y变化到最大值的方向。最后的结果形式与相反（转置），若是列向量，那么结果就是行向量。

而若是向量形式的，那么结果的形式与的形式相同，不用转置。

在机器学习/深度学习领域，一般是自动求导的，不需要人工计算。

计算图：类似链式法则，每一步取子式建立操作子，生成有向无环图。

自动梯度的实现（当然可以调现成的包）

计算y关于x的梯度：

首先需要一个地方存储梯度：

两种方法是等价的。

计算y：

这儿有一个grad_fn，gradient function表示这是一个y关于x的梯度值，因为pytorch是隐式构造的计算图。

通过调用反向传播函数backward()可以自动计算y关于x每个分量的梯度，因为反向传播其实是传统链式法则数学解法的逆，而x.grad中按照链式法则存储了每一个操作子的结果：

可以看到结果和4 * x（y关于x的导数）是一致的：

试一下对向量的sum求梯度，当然，向量求和的梯度都是1，因为向量求和相当于xE，y = xE中，y对x求导的结果就是E，但是操作之前需要用.grad.zero_()来对.grad内的数据清零（其实是写进0）：

在深度学习中，我们常常不去计算矩阵的导数，很少对向量的函数求导，而是要求对每个样本单独计算的导数之和（对标量求导），因为最终要求的都是loss，如果loss是一个向量，求一次梯度就变成一个二维矩阵，再延申一层就变成四维的，如果神经网络的层数很深，那最后就会变成一个很大的张量，自然会很麻烦，所以对于向量，一般一开始就先求一个sum，让向量变成一个标量，再进行求导：

可以通过把某一个函数detach掉，使它变成一个常量，就可以将它移动到记录的计算图之外，在训练模型中需要固定某个值的时候很管用：

显而易见，y是一个关于x的函数，而u只是一个值等于x * x的常量，所以在z对x求导的时候，只剩下了u。

那再对y求一次导看看：

意料之中的结果。

即使构建函数的计算图需要通过python控制流（条件、循环或任意函数调用），我们仍然可以计算得到变量的梯度：

线性回归的实现：

（需要安装d2l包：pip install d2l）

先做好把数据传到matplotlib的准备：

随机生成一个数据集，X从0到1取随机值，y在线性回归的基础上在加上一个从0到1之间取随机值的随机噪声，将X和y都以列向量的形式return，样本值w取[2, -3.4]，偏差b取4.2，最后把X和y分别赋值给特征features和标签labels：

可以看一下特征和标签里的第0个值：

既然用了matplotlib，也可以画一下图像：

其中，必须先detach才可以送到numpy。

然后定义一个data_iter函数（迭代器），该函数接受批量大小、特征矩阵和标签向量作输入，生成大小为batch的小批量。首先取特征矩阵的长度（特征的个数），再通过range生成一个随机标号的list，叫indices，之后对每一个i求一个batch_size（=10）：

数据集定义完了，接下来定义模型。

定义模型首先需要初始化参数，其中w是一个向量，b是一个标量，两个变量都需要做优化求导，所以都需要requires_grad=True：

定义模型：

定义损失函数（均方误差，y_hat是预测值，对应模型的输出，y是真实值，对应labels。但这里不完整，没求和）：

定义优化算法（小批量随机梯度下降，lr是learning rate学习率）：

在梯度下降最后需要把param.grad置零，保证每次下降互相独立。

定义训练函数：

（每一次epoch都对所有的数据做一遍计算，每一次计算中，l都是长为批量大小的向量）

可以看出每一次迭代，最后的损失都会越来越小，将真实参数与模型预测的参数做比较来评估训练的成功程度：

整个过程中，lr和num_epochs就是所谓的超参数，需要人工指定，可以尝试一下不同的学习率和epoch次数对最后的loss都有什么影响（每次重新跑之前都需要重新初始化w和b）。

线性回归的简洁实现（使用现成的模块）：

调用框架现有API来读取数据：

使用框架定义好的层（nn是神经网络neural network的缩写，nn中有大量定义好的层，可以直接使用，nn.Linear(*, *)需要指定输入和输出的维度，然后把它放到一个叫Sequential的容器当中，相当于list of layers）：

初始化模型参数（0读取到Linear，weight读取到w，data读取真实值，normal_用正态分布替换真实值）：

均方误差：

实例化SGD（Stochastic Gradient Descent：随机梯度下降）实例：

训练结果：

用牛顿法（求二阶导）可以比随机梯度下降的梯度下降更快，但是很多时候梯度下降快并不一定是个好事，就像学习率，而且算二阶导很贵，所以一般用跟学习率相配合的SGD。